Strategies
King, Knight, and King/Knight Sudoku puzzles are solved using a combination of standard sudoku strategies and extra constraints. Here are some strategies to help you solve these puzzles:
Standard Sudoku Strategies
Standard sudoku rules apply to these puzzles - each row, column, and region must contain the numbers 1-9 once and only once. This allows us to make some deductive reasoning, based on what possible numbers are available in each cell. For example:
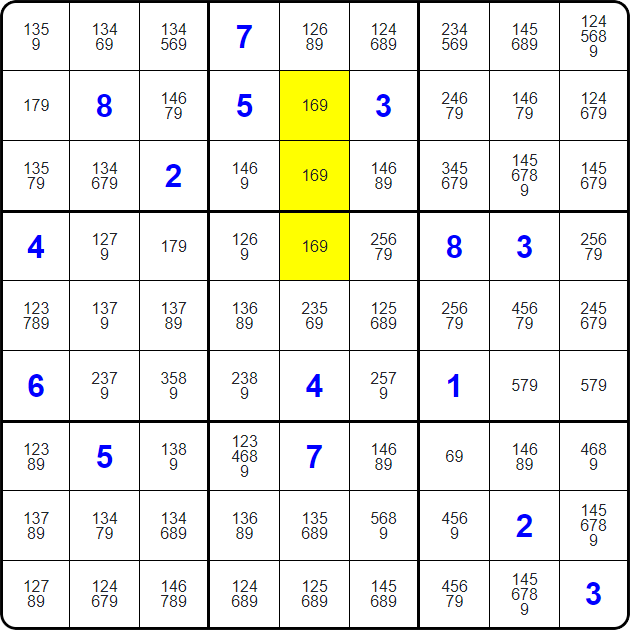
Since these three squares must be a 1, a 6, and a 9, regardless which is which...
None of the marked cells here can have a 1, a 6, or a 9. We can remove those hints.
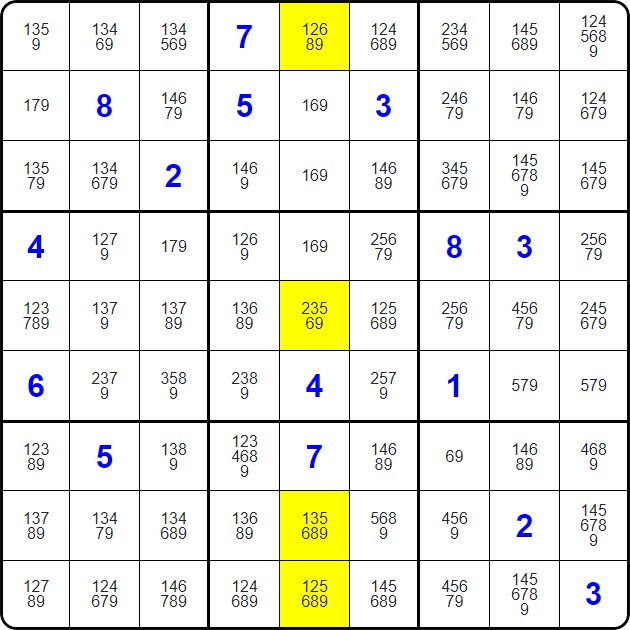
Or since these three squares must be a 1, a 7, and a 8, and they are all in the same column AND the same region...
We can clear all of these marked hints in the region and the column, eliminating the 1s, 7s, and 8s.
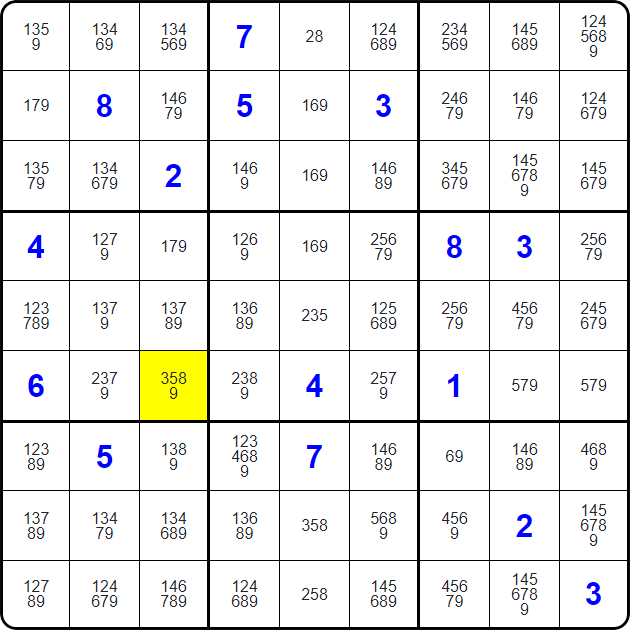
Sometimes you will find yourself playing hide-and-seek within the hints as well. Inside its region, the highlighted cell is the only one that has 5 as a possibility - therefore, the 5 MUST go there.
Chess Constraint Strategies
Sometimes, the extra constraints can be used to eliminate possibilities in a way that standard sudoku strategies can't. Here are some examples of using the extra constraints, based on a sample Knight Rule puzzle:
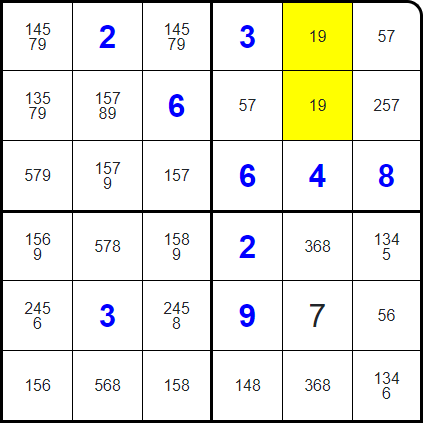
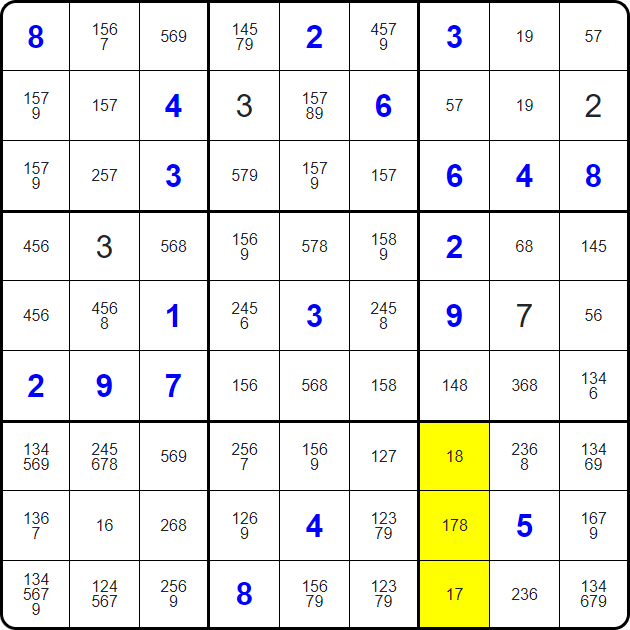
For example, in the top left region, there is a 1-9 pair. "Pointing Partners" above already indicates that there cannot be another 1 or 9 in this column, since they are aligned vertically. However, since this is a knight rule puzzle...
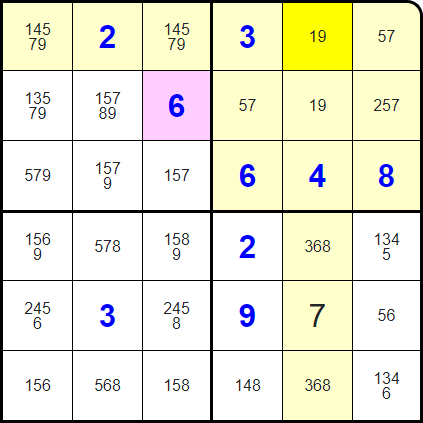
None of these squares can contain a 1 or a 9...
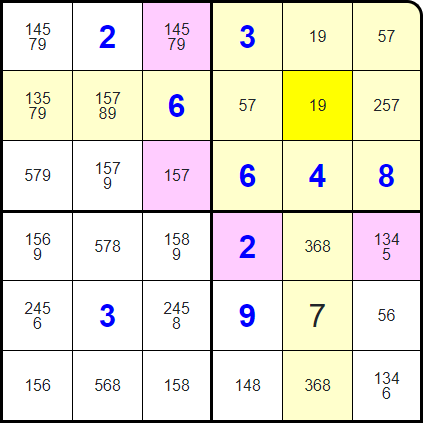
...and neither can any of these!
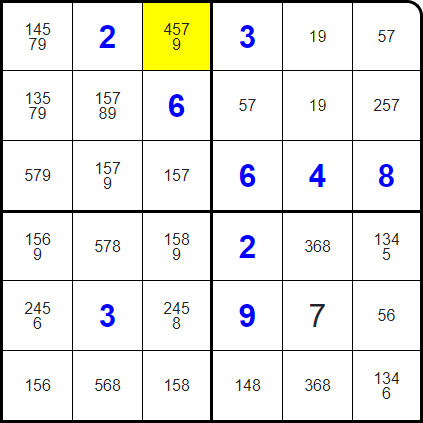
Since this highlighted square is affected by both of the cells above (for different constraints), it cannot contain a 1 or a 9!
Here's a slightly more complex example:
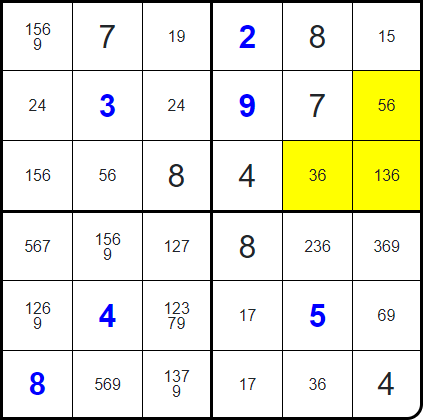
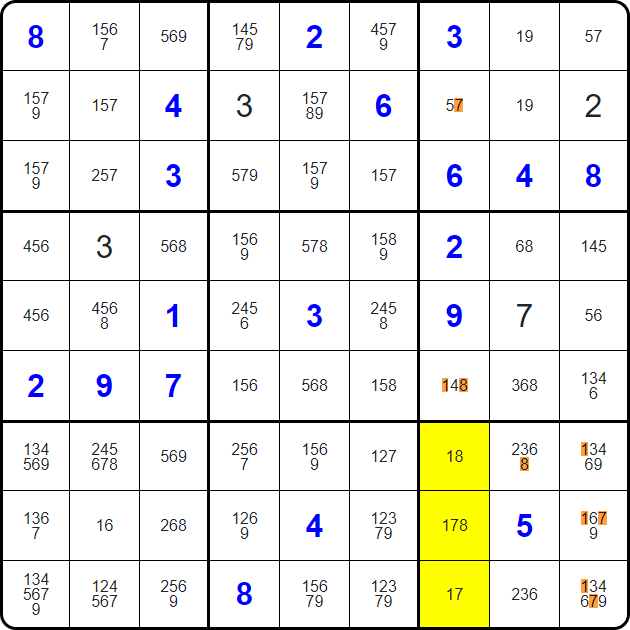
In the top-right region, the highlighted squares are the only ones that can contain a 6. One by one, we'll look at the squares that each of them impact:
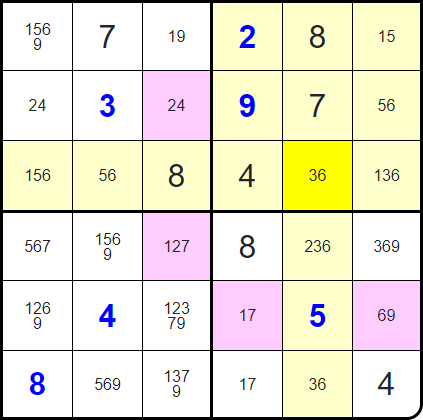
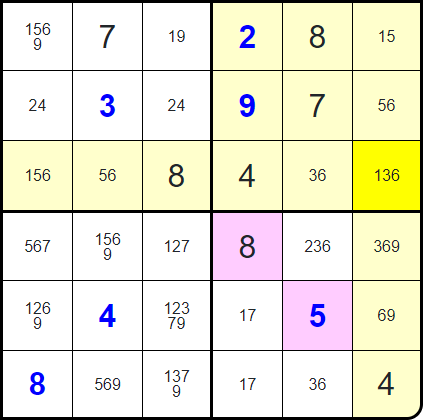
Do you see where they all overlap?

That cell cannot contain a 6 - meaning it must be a 9!